Cours de maths : le raisonnement par récurrence
Pour démontrer une propriété mathématique, on a plusieurs formes de raisonnements. On cite en guise d'exemple : le raisonnement par l'absurde, le raisonnement par contraposée, raisonnement par disjonction des cas... Aujourd'hui, dans ce cours de maths, nous allons nous intéresser au raisonnement par récurrence. Cette forme de raisonnement a la particularité de démontrer des propriétés portant sur tous les entiers naturels !
Étudions ensemble un exemple :
Supposons qu'on a à démontrer la propriété suivante :
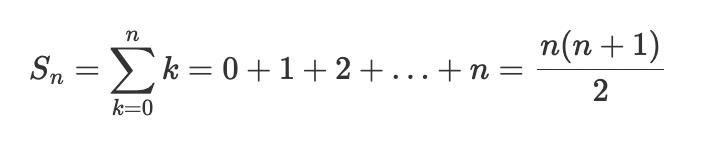
Petit tour historique :
On présume qu'un jour, un enseignant a demandé à ses élèves de calculer la somme suivante :
0 + 1 + 2 + 3 + ... + 100
L'enseignant pensait que cela prendrait de longues minutes à ses élèves pour pouvoir résoudre ce problème, surtout qu'ils étaient très jeunes. Sauf que Johann Karl Friedrich Gauss, un des élèves présents, a immédiatement répondu que le résultat valait 5050 ! Le résultat est bien correct et ce fameux Gauss est devenu un mathématicien très très célèbre !
Comment a-t-il trouvé ce résultat ?
Découvrons ceci ensemble avant de passer au raisonnement par récurrence.
On note A = 0 + 1 + 2 + 3 + 4 + 5 + ... + 100
L'addition est une opération commutative, cela veut dire que l'ordre n'est pas très important.
1 + 2 = 2 + 1
Sous ce principe, on peut dire que :
A est aussi = à : 100 + 99 + 98 + 97 + 96 + 95 + ... + 1 + 0
mettons ces deux expressions l'une en dessous de l'autre:
A = 0 + 1 + 2 + 3 + 4 + 5 +... + 100
A = 100 + 99 + 98 + 97 + 96 + 95 + ... + 1
En additionnant les deux expressions, on trouve :
2A = 100 + 100 + 100 + 100 + 100 + ... + 100
On pourrait se poser la question : combient de fois le "100" apparaît-il ?
On remarque qu'il apparaît 101 fois ! "car on commence de 0.
Donc, on trouve :
2A = 101 x 100 = 10100
D'où :
A = 10100 / 2 = 5050
On retrouve bien la fameuse réponse de Gauss !
Ce calcul peut alors être généralisé.
Au lieu de calculer la somme de 0 jusqu'à 100, on voudrait savoir le résultat si on calcule la somme de 0 jusqu'à un entier naturel n.
Revenons à notre propriété. Cette propriété nous dit que la somme 0 + 1 + 2 + ... + n = n x (n+1) /2 et ce pour tout n entier naturel.
"Vous pouvez bien vérifier qu'elle est correcte pour 100."
Le raisonnement par récurrence est un principe qui nous aide à démontrer les propriétés de ce type. Vous imaginez bien qu'on ne va pas essayer de vérifier la formule pour tous les entiers, pour la simple et unique raison qu'il existe une infinité d'entiers !
La méthode de la récurrence vient alors nous aider et voici comment on procède :
Étape 1 : "Initialisation"
Dans cette étape, on vérifie que la propriété est correcte pour le premier entier possible étant n = 0. Dans ce cas on veut additioner 0 avec... rien , ce qui fait 0. Et on a bien: 0 x (0+1) / 2 = 0
La propriété est donc bien vérifié pour n = 0
Étape 2 : "Hérédité"
Dans cette étape, on suppose que notre propriété est vraie au rang n, cela veut dire qu'on suppose qu'elle est vraie pour un entier naturel n.
Ensuite, il faut montrer que la propriété est vraie au rang n+1.
Voici la procédure à suivre :

Étape 3 : "Conclusion"
On récapitule ce qu'on a fait en disant que la propriété est vraie au rang 0. On l'a supposé vraie au rang n et on a démontré qu'elle est vraie au rang n+1, donc par principe de récurrence la propriété est vraie.
Et voilà, on a démontré par récurrence ce problème !

