Cours de maths terminale : calcul des primitives d'une fonction

Cet article s'adresse prioritairement aux élèves en classe de terminale, suivant la spé maths. Il est consacré, comme son titre l'indique, au calcul des primitives d'une fonction qui interviennent de façon pratique dans le calcul d'intégrales et dans la résolution des équations différentielles et en particulier, celles que l'on rencontre en physique-chimie.

Bien que ce cours de maths soit destiné aux élèves de terminale, les étudiants en classes supérieures pourront également y trouver un intérêt très particulier.

Nos professeurs particuliers

Stéphanie (8)10100

Diana 1^er cours offert (5)10100

Position du problème

Soit f : I ⟶ ℝ une fonction définie sur un intervalle I de ℝ.  On cherche à déterminer s’il existe une fonction F : I ⟶ ℝ dérivable sur I dont la dérivée est f ; c’est-à-dire telle que F’ = f.

Si une telle fonction F existe (et c’est le cas si la fonction f est continue sur I), on dit que F est une primitive de f sur l’intervalle I.

POINT N°1 : Définition et propriétés

Mise en œuvre :

Cours de maths en ligne

Mise en œuvre :

POINT N°2 : Calcul des primitives

Le calcul des primitives est un problème très délicat (de façon générale) et qui repose sur les formules des primitives usuelles déduites de celles des dérivées. Le tableau présenté ci-dessous donne les principales primitives usuelles.

NOTE : Pour trouver les primitives d'une fonction donnée, il suffit d'appliquer de manière adéquate une ou plusieurs de ces formules ; ce qui impose de bien les connaître. Dans les exercices suivants intitulés "APPLICATION", il s'agit de mettre en oeuvre ces différentes formules pour déterminer des primitives.

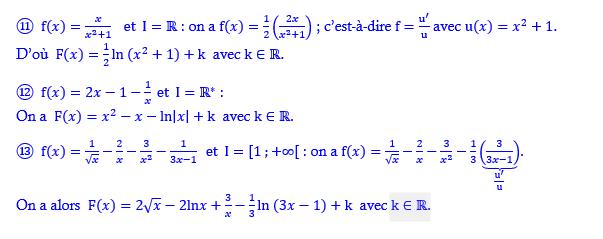
POINT N°3 : Un peu de vocabulaire sur les équations différentielles

• On appelle équation différentielle sur un intervalle I de ℝ, toute équation (E) dans laquelle intervient une fonction inconnue y dérivable sur I et au moins une de ses dérivées successives.
• On appelle alors ordre de l'équation différentielle (E), l'ordre le plus élévé de la dérivée avec lequel la fonction inconnue y apparait dans l'équation différentielle (E).
• Résoudre (ou intégrer) l'équation différentielle (E) sur I, consiste alors à trouver toutes les fonctions solutions de (E) ; c'est-à-dire toutes les fonctions y définies et dérivables sur I vérifiant l'équation différentielle (E).

Trouvez votre prof à domicile ICI

Par exemple, l'équation (E) : y' - 2y =3 est une équation différentielle du premier ordre sur ℝ.

L'équation (E) : y'' - 3y' + 2y=0 est une équation différentielle du second ordre sur ℝ.

Les équations différentielles élémentaires sont étudiées en classe de terminale en spécialité mathématiques, mais nous ne les abordons pas dans cet article. Contentons-nous, cependant, de montrer leur lien avec les primitives.

Soit f : I ⟶ ℝ une fonction définie sur un intervalle I de ℝ.  Considérons alors sur I, l'équation différentielle du premier ordre  (E) : y' = f(x) d'inconnue y : I ⟶ ℝ. 

Il est alors clair que les solutions de cette équation différentielle (E) sont les fonctions y dérivables sur I et dont la dérivée est la fonction f ; c'est-à-dire les primitives de f sur I.

CONSÉQUENCE : Si F est une primitive de f sur I, alors les solutions de l'équation différentielle (E) : y' = f(x) sont les fonctions y : I ⟶ ℝ définies par y(x) = F(x) + k avec k une constante réelle.

EXEMPLE 1 : Résoudre sur ℝ l'équation différentielle (E) : y' = cos(x) - sin(x).

Une primitive sur ℝ, de la fonction f définie sur ℝ par f(x)= cos(x) - sin(x) est la fonction F définie sur  ℝ par F(x)= sin(x) + cos(x). On en déduit que les solutions de l'équation différentielle (E) sont les fonctions y : ℝ⟶ ℝ définies par y(x)= sin(x) + cos(x) + k  avec k une constante réelle.

EXEMPLE 2 : Soit a un nombre réel non nul. Considérons sur ℝ l'équation différentielle (E) : y' = ay.

Alors y est solution de (E) si et seulement si pour tout x de ℝ, y'(x) - ay(x) = 0 ; c'est-à-dire si et seulement si [y'(x) - ay(x)]exp(-ax) = 0 car pour tout x de ℝ, exp(-ax) est non nul.

Ce qui aquivaut à y'(x)exp(-ax) - ay(x)exp(-ax) = 0 pour tout x de ℝ.

Or, on voit facilement que le terme de gauche n'est autre que la dérivée de la fonction u définie sur ℝ par u(x) = y(x)exp(-ax).

Donc y est solution de (E) si et seulement si pour tout x de ℝ, u'(x) = 0  ; ce qui équivaut à dire que la fonction u est constante ; c'est-à-dire qu'il existe un réel k tel que pour tout x de ℝ, u(x) = k.

Or u(x) = k si et seulement si y(x)exp(-ax) = k ; ce qui équivaut à y(x) = kexp(ax). Donc y est solution de (E) si et seulement si pour tout x de ℝ, y(x) = kexp(ax) avec k une constante réelle.

CONSÉQUENCE : Soit a un nombre réel non nul. Alors les solutions de l'équation différentielle (E) : y' = ay sur ℝ sont les fonctions y : I ⟶ ℝ définies par y(x) = k.exp(ax) avec k une constante réelle, exp désignant la fonction exponentielle.